関数従属性と関数従属性の推論則

はじめに

関数従属性についてまとめました。

関数従属性

項目Xの値を決定すると、項目Yの値が一つに決定されるとき、

項目Yは項目Xに関数従属しているといいます。

これをX→Yと表記し、Xを決定項、Yを被決定項といいます。

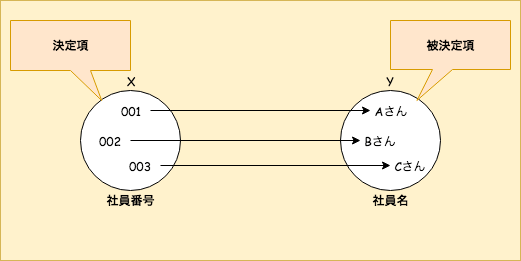
上の図の例では、

社員に対して一意に振られている社員番号が決まれば、

社員の名前が決まるというケースを挙げています。

関数従属性の推論則

関数従属性には、次のような推論則が成立します。

(次の、X、Y、Z、及びWは、属性集合です)

反射律

YがXの部分集合ならば、X→Yが成立する。

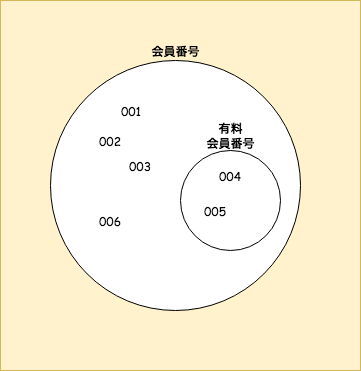
上の図の例では、

会員番号の中に、部分集合として有料会員番号があることを表しています。

会員番号004が決まれば、有料会員番号004が決まります。

増加律

X→Yが成立するならば、{X, Z}→{Y, Z}が成立する。

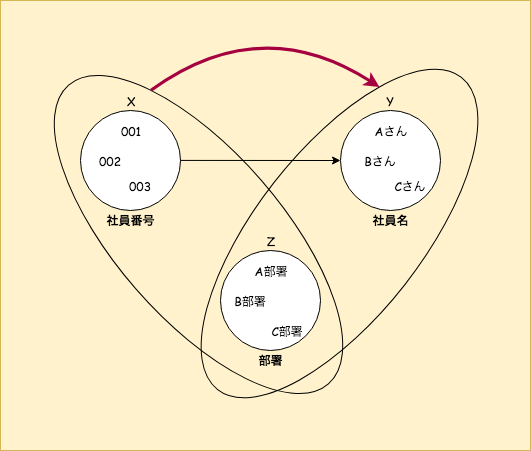
上の図の例では、

社員番号が決まれば社員名が決まり、

社員番号と部署が決まれば、社員名と部署が決まることを表しています。

推移律

X→Yかつ、Y→Zが成立するならば、X→Zが成立する。

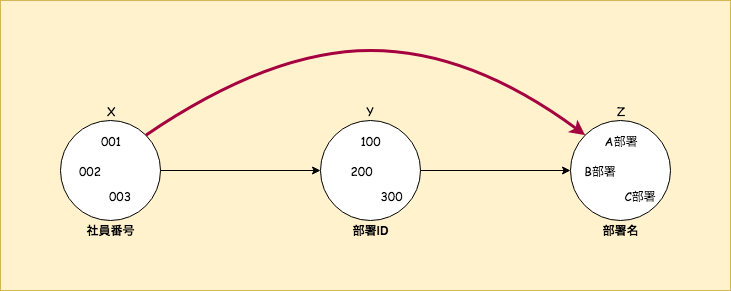
図の上の例では、

社員番号が決まれば部署IDが決まり、

部署IDが決まれば部署名が決まるという前提があり、

社員番号が決まれば部署名が決まることを表しています。

擬推移律

X→Yかつ、{W, Y}→Zが成立するならば、{W, X}→Zが成立する。推移律はWが空集合の場合である。

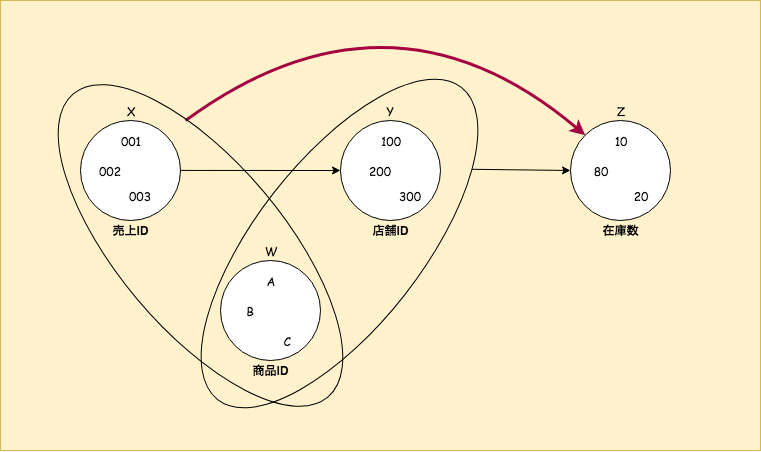
上の図の例では、

まず、売上IDが決まると店舗IDが決まり、(どこの店舗の売上かを管理)

店舗IDと商品IDから在庫数が決まる(ある店舗のある商品の在庫数を管理)という前提があり、

その場合、売上IDと商品IDから在庫数が決まるということを表しています。

合併律

X→YかつX→Zが成立するならば、X→{Y, Z}が成立する。

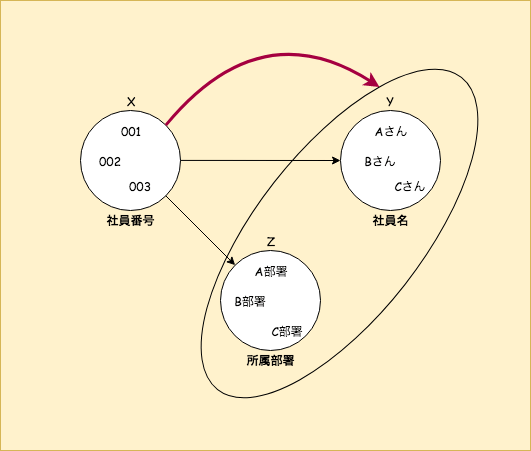
上の図の例では、

社員番号が決まれば、社員名、所属部署がそれぞれ決まる場合、

社員番号が決まれば社員名と所属部署が同時に決まることを表しています。

分解律

X→{Y, Z}が成立するならば、X→YかつX→Zが成立する。

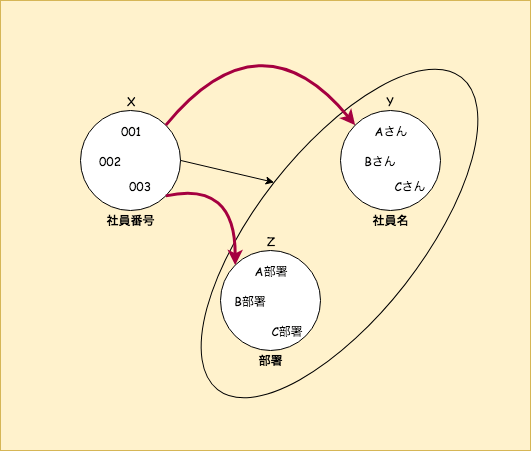
上の図の例では、

社員番号が決まれば、社員名と所属部署が同時に決まる場合、

社員番号が決まれば社員名、所属部署がそれぞれ決まることを表しています。

おわりに

今回は関数従属性とは何か、

また、関数従属性の推論則について確認しました。

おまけ

現場で使えるデータベース周りのナレッジまとめ記事を作ったので

是非そちらも参照ください！！

初めてデータベースを触る方に向けて〜新人プログラマー時代の自分に伝えたいこと〜